해당 글은 현재 수강중인 수업 내용을 정리한 것을 밝힙니다.
우선 비지도학습에 대해 간단히 설명하자면 Taget이나 Label이 없는 상태에서 나머지 특성들 가지고 예측하려고 하는 것입니다. 이러한 비지도 학습에는 군집화, 차원축소, 시각화가 있습니다.
군집화 같은 경우에는 고객 Segmentation 즉, 고객군별 마케팅 전략으로 사용하거나 이상치를 탐지할 때 사용합니다.
차원축소는 특성의 가짓 수가 굉장히 많을 때(예를 들어 Image Data) 중요한 것들로 줄여나가야 할 때 차원축소 문제라고 합니다.
오늘은 비지도학습 중 군집화에 대해서 정리해보려고 합니다.
군집화란?
주어진 데이터들을 비슷한 것끼리 나누어 그룹을 만드는 것입니다.
종류
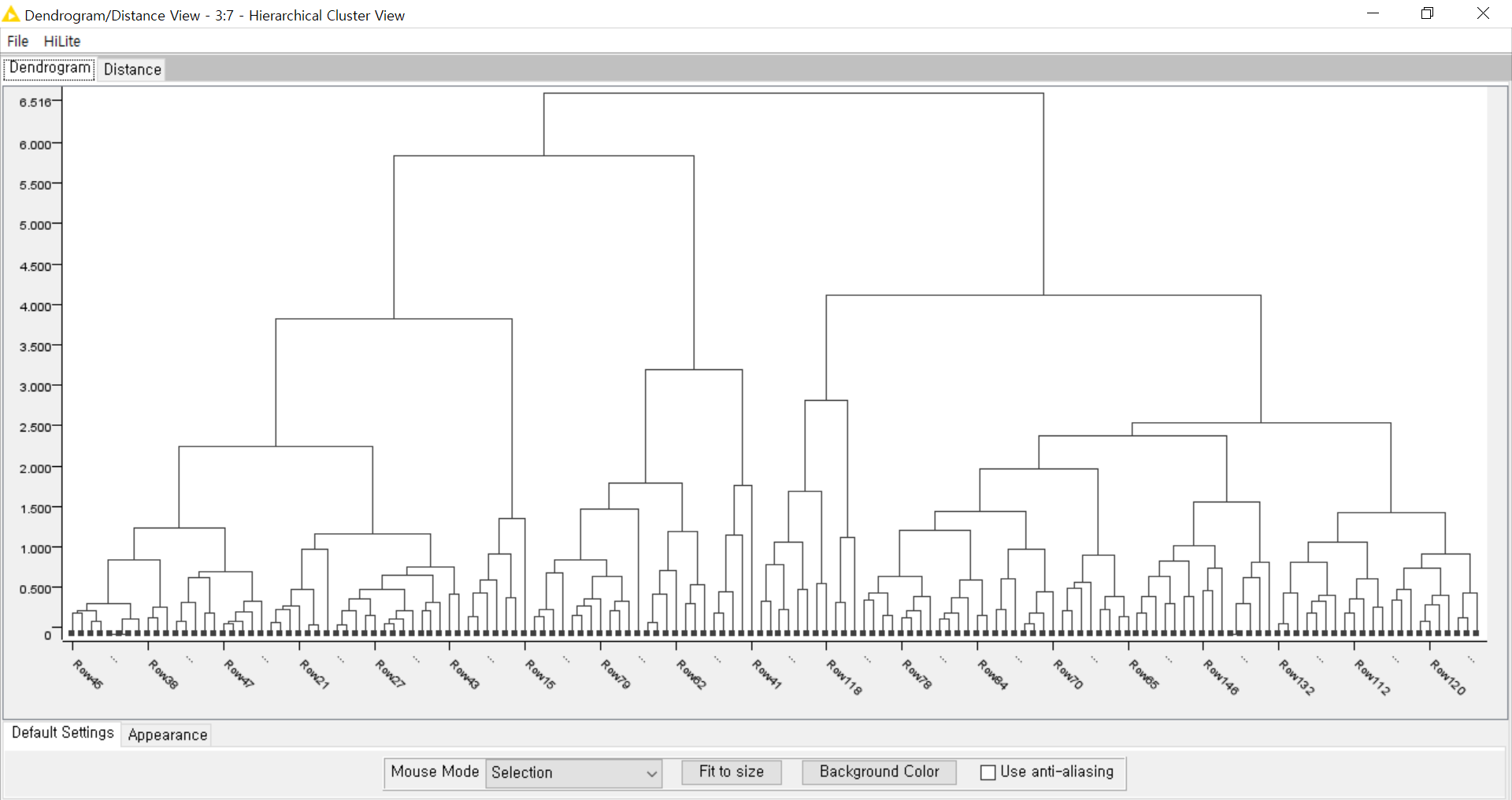
- Linkage Based
Data들을 묶어서 묶은 것을 또 묶으면서 연결시켜 나가는 것입니다. 묶는 것, 연결된 선을 Link라고 보면 됩니다. Link들로 서로 가까움과 먼 정도를 표시해서 군집을 만들어 나가는 것입니다.
Linkage Based의 대표적인 알고리즘은 Hierarchical clustering (계층적 군집화)입니다.

- Density based Clustering
Density는 밀도입니다. 조밀하게 가까이 모여있는 것을 밀도가 높다고 합니다. 밀도가 높게 모여있는 부분으로 구분합니다.
Density based Clustering의 대표적인 알고리즘은 DBSCAN입니다.

- Partitioning
경계면을 만들어 나가는 것을 Partitioning이라고 합니다. 경계선을 만들어서 집단들을 나누는 방법입니다. 묶는 것을 찾는 것이 아니라 경계선을 찾아서 서로 다른 군집이라는 것을 구분해내는 것입니다.
Partitioning의 대표적인 알고리즘은 K-Means입니다.
Distance
Clustering을 할 때 중요한 개념 중 하나가 Distance 즉, 거리 개념입니다. 거리 개념에 대해 간단하게 짚고 넘어가겠습니다.

- Euclidean Distance (유클리디안 거리) & Manhattan-Distance (맨해튼 거리)
유클리디안 거리는 2개의 점 사이에 가장 짧은 직선을 그린 거리입니다. 맨해튼 거리는 x축의 거리와 y축의 거리 각각을 계산해서 더한 것입니다. 직교 거리라고 합니다.
-> 이 두 거리를 대표적으로 사용합니다!
이외에도 Minkowski-Distance가 있습니다. 차원을 p차원으로 증가시켜서 계산한 것입니다. p=1이면 Manhattan-Distance가 되고, p=2면 Euclidean Distance가 됩니다.
- Maximum-Distance (맥시멈 거리)
위 거리들과 달리 p값이 무한대입니다. 많은 점들 중 가장 먼 점들 사이의 거리를 말합니다.
최적의 클러스터링은?
군집 내 거리 가까워야 하고 군집 사이 거리 멀어야 합니다.
내부의 거리는 Within-Cluster Variation라고 하고, Cluster 사이의 거리는 Between-Cluster Variation이라고 합니다.
Clustering Quality
성능지표의 식을 알아보겠습니다.CQ = Between-Cluster Variation / Within-Cluster Variation 입니다.CQ가 높은 것이 Clustering이 잘 된 것이라고 볼 수 있습니다.
실루엣 계수(Silhouette-Coefficient For Object x)
실루엣은 전체적인 모양이나 윤곽을 뜻합니다. Cluster의 모양이 어떻게 엮여져 있는지 알아보는 척도입니다. one by one으로 계산합니다.
클러스터 a에 한 점인 i가 있다고 가정합시다. 우선, 점 i가 속한 클러스터 a 내 다른 점과의 거리들의 평균을 구합니다. 그 다음 다른 클러스터 b, c 내의 점들과의 각각의 거리를 계산해서 평균을 냅니다.
점 i가 속하지 않은 클러스터 b, c의 점 중 가장 짧은 평균거리를 가진 것을 b(i)라고 합시다. 자신이 속한 클러스터 내의 거리 평균을 a(i)라고 합니다.실루엣 계수 S(i) = b(i) - a(i) / max{a(i), b(i)} 이 식의 값을 실루엣 계수라고 합니다. 실루엣 계수의 값은 -1보다 크거나 같고, 1보다 작거나 같습니다. 1에 가까울수록 구분을 잘 된 것이고, 0에 가까우면 구분이 잘 안 된 것이고, 마이너스에 가까우면 엉터리로 된 것이라고 생각하면 됩니다.
다음 포스팅은 군집화 모델들을 설명해보겠습니다.
'ETC > School' 카테고리의 다른 글
| [DB 구축 및 활용]/[이론] 데이터 타입 (feat. Oracle) (0) | 2022.04.09 |
|---|
해당 글은 현재 수강중인 수업 내용을 정리한 것을 밝힙니다.
우선 비지도학습에 대해 간단히 설명하자면 Taget이나 Label이 없는 상태에서 나머지 특성들 가지고 예측하려고 하는 것입니다. 이러한 비지도 학습에는 군집화, 차원축소, 시각화가 있습니다.
군집화 같은 경우에는 고객 Segmentation 즉, 고객군별 마케팅 전략으로 사용하거나 이상치를 탐지할 때 사용합니다.
차원축소는 특성의 가짓 수가 굉장히 많을 때(예를 들어 Image Data) 중요한 것들로 줄여나가야 할 때 차원축소 문제라고 합니다.
오늘은 비지도학습 중 군집화에 대해서 정리해보려고 합니다.
군집화란?
주어진 데이터들을 비슷한 것끼리 나누어 그룹을 만드는 것입니다.
종류

- Linkage Based
Data들을 묶어서 묶은 것을 또 묶으면서 연결시켜 나가는 것입니다. 묶는 것, 연결된 선을 Link라고 보면 됩니다. Link들로 서로 가까움과 먼 정도를 표시해서 군집을 만들어 나가는 것입니다.
Linkage Based의 대표적인 알고리즘은 Hierarchical clustering (계층적 군집화)입니다.

- Density based Clustering
Density는 밀도입니다. 조밀하게 가까이 모여있는 것을 밀도가 높다고 합니다. 밀도가 높게 모여있는 부분으로 구분합니다.
Density based Clustering의 대표적인 알고리즘은 DBSCAN입니다.

- Partitioning
경계면을 만들어 나가는 것을 Partitioning이라고 합니다. 경계선을 만들어서 집단들을 나누는 방법입니다. 묶는 것을 찾는 것이 아니라 경계선을 찾아서 서로 다른 군집이라는 것을 구분해내는 것입니다.
Partitioning의 대표적인 알고리즘은 K-Means입니다.
Distance
Clustering을 할 때 중요한 개념 중 하나가 Distance 즉, 거리 개념입니다. 거리 개념에 대해 간단하게 짚고 넘어가겠습니다.

- Euclidean Distance (유클리디안 거리) & Manhattan-Distance (맨해튼 거리)
유클리디안 거리는 2개의 점 사이에 가장 짧은 직선을 그린 거리입니다. 맨해튼 거리는 x축의 거리와 y축의 거리 각각을 계산해서 더한 것입니다. 직교 거리라고 합니다.
-> 이 두 거리를 대표적으로 사용합니다!
이외에도 Minkowski-Distance가 있습니다. 차원을 p차원으로 증가시켜서 계산한 것입니다. p=1이면 Manhattan-Distance가 되고, p=2면 Euclidean Distance가 됩니다.
- Maximum-Distance (맥시멈 거리)
위 거리들과 달리 p값이 무한대입니다. 많은 점들 중 가장 먼 점들 사이의 거리를 말합니다.
최적의 클러스터링은?
군집 내 거리 가까워야 하고 군집 사이 거리 멀어야 합니다.
내부의 거리는 Within-Cluster Variation라고 하고, Cluster 사이의 거리는 Between-Cluster Variation이라고 합니다.
Clustering Quality
성능지표의 식을 알아보겠습니다.CQ = Between-Cluster Variation / Within-Cluster Variation 입니다.CQ가 높은 것이 Clustering이 잘 된 것이라고 볼 수 있습니다.
실루엣 계수(Silhouette-Coefficient For Object x)
실루엣은 전체적인 모양이나 윤곽을 뜻합니다. Cluster의 모양이 어떻게 엮여져 있는지 알아보는 척도입니다. one by one으로 계산합니다.
클러스터 a에 한 점인 i가 있다고 가정합시다. 우선, 점 i가 속한 클러스터 a 내 다른 점과의 거리들의 평균을 구합니다. 그 다음 다른 클러스터 b, c 내의 점들과의 각각의 거리를 계산해서 평균을 냅니다.
점 i가 속하지 않은 클러스터 b, c의 점 중 가장 짧은 평균거리를 가진 것을 b(i)라고 합시다. 자신이 속한 클러스터 내의 거리 평균을 a(i)라고 합니다.실루엣 계수 S(i) = b(i) - a(i) / max{a(i), b(i)} 이 식의 값을 실루엣 계수라고 합니다. 실루엣 계수의 값은 -1보다 크거나 같고, 1보다 작거나 같습니다. 1에 가까울수록 구분을 잘 된 것이고, 0에 가까우면 구분이 잘 안 된 것이고, 마이너스에 가까우면 엉터리로 된 것이라고 생각하면 됩니다.
다음 포스팅은 군집화 모델들을 설명해보겠습니다.
'ETC > School' 카테고리의 다른 글
| [DB 구축 및 활용]/[이론] 데이터 타입 (feat. Oracle) (0) | 2022.04.09 |
|---|
